MATEMATICA

GENERADOR DE FUNCIONES

OBJETIVO GENERAL DE LA SECUENCIA

Que los estudiantes conceptualicen y comprendan el concepto de función como una relación entre variables (dependiente e independiente) a través de sus diferentes representaciones: pictórica, numérica, tabular y algebraica mediante el simulador “Generador de funciones”

DESARROLLO

Las funciones algebraicas son aquellas cuya regla de correspondencia es una expresión algebraica, siendo a la vez una función que satisface una ecuación polinómica cuyos coeficientes son a su vez polinomios.

Una función algebraica explícita es aquella cuya variable y se adquiere combinando un número finito de veces la variable x y constantes reales a partir de operaciones algebraicas de suma, resta, multiplicación, división, elevación a potencias y extracción de raíces. Entonces en las funciones explicitas es posible obtener las imágenes de x por sustitución:

f(x) = 5x – 2

Las funciones polinómicas de primer grado se definen como:

f(x) = mx +n

Donde "m" es la pendiente de la recta. La pendiente es la inclinación de la recta con respecto al eje de abscisas.

Para reforzar mira el siguiente VIDEO

Experimenta en PHET 

Desarrolla la siguiente actividad en LIVEWORKSHEETS  

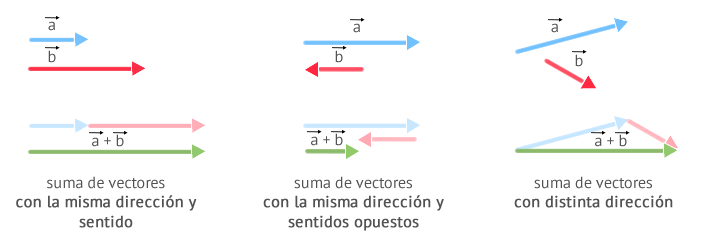
  ADICIÓN DE VECTORES

Como los vectores tienen módulo y dirección, la suma de vectores no sigue las reglas de la suma tradicional de los escalares. De forma gráfica, la suma de dos vectores $\overrightarrow{�}$ y $\overrightarrow{�}$ nos dará como resultado otro vector $\overrightarrow{�}$ que podemos obtener mediante 2 métodos distintos: el método de la cabeza con cola (o del extremo con origen) y la regla del paralelogramo.

Método de la cabeza con cola.

Respetando la dirección y sentido de ambos vectores,

1. Desplazamos el vector $\overrightarrow{�}$ de tal forma que su origen se encuentre a continuación del extremo de $\overrightarrow{�}$.
2. $\overrightarrow{�}$ será el segmento recto que podamos dibujar desde el origen de $\overrightarrow{�}$ hasta el extremo de $\overrightarrow{�}$.

Para reforzar mira el siguiente VIDEO

Experimenta en PHET para conocer mejor la adición de vectores 

Desarrolla la siguiente actividad en LIVEWORKSHEETS  

FRACCIONES EQUIVALENTES

Las fracciones equivalentes son aquellas que representan la misma cantidad, pero se expresan de diferentes maneras. En otras palabras, dos o más fracciones son equivalentes si representan la misma cantidad de algo. Por ejemplo, las fracciones 1/2 y 2/4 son equivalentes, porque ambas representan la mitad de algo.

Características de las fracciones equivalentes:

Las fracciones equivalentes tienen varias características importantes que vale la pena conocer:

1. Las fracciones equivalentes representan la misma cantidad, pero se expresan de diferentes maneras. Esto significa que el valor numérico de las fracciones es el mismo.
2. Para obtener fracciones equivalentes, podemos multiplicar o dividir el numerador y el denominador por el mismo número. Esto se conoce como simplificación o reducción de fracciones.
3. Podemos expresar una fracción en forma de fracción decimal o porcentaje, y aún así mantener su equivalencia.
4. Las fracciones equivalentes son muy útiles en la resolución de problemas matemáticos, ya que nos permiten trabajar con fracciones de diferentes denominadores.

Para reforzar mira el siguiente VIDEO

Experimenta en PHET 

Desarrolla la siguiente actividad en LIVEWORKSHEETS

  

PENDIENTE DE UNA FUNCIÓN

Para calcular la pendiente de una función es necesario comprender la fórmula para la pendiente, y esto se define como "la altura sobre la longitud", siendo la altura la distancia vertical entre dos puntos y la longitud la distancia horizontal entre dos puntos.

Empecemos eligiendo dos puntos en la línea y etiquétalos con sus coordenadas. Puedes elegir dos puntos cualquiera a través de los cuales se extienda la línea.

• Las coordenadas se escriben como ${\displaystyle (�,�)}$, siendo ${\displaystyle �}$ la ubicación a lo largo del eje x (o el eje horizontal) e ${\displaystyle �}$ la ubicación a lo largo del eje y (o el eje vertical).
• Por ejemplo, podrías optar por dos puntos cuyas coordenadas sean ${\displaystyle (3,2)}$ y ${\displaystyle (7,8)}$

Determina cuál es el orden de los puntos. Uno de ellos será el punto 1 y el otro será el punto 2. No tiene importancia cuál de los dos sea cuál, tan solo debes asegurarte de que se mantengan en el orden correcto a lo largo de todo el cálculo.

Las coordenadas del primer punto serán  y las del segundo serán 

Dispón la fórmula para la pendiente. Esta es ${\displaystyle \frac{���������}{��������}=\frac{{�}_2-{�}_1}{{�}_2-{�}_1}}$. 

reemplazando los datos tendremos  y esto es igual a 6/4, simplificando tendremos 3/2 lo que vendría a ser la pendiente de la función con los puntos dados.

Para reforzar mira el siguiente VIDEO

Experimenta en PHET 

Desarrolla la siguiente actividad en LIVEWORKSHEETS

IGUALDAD - ECUACIONES  

En esta lección vamos a ver las ecuaciones. A partir de aquí empieza la diversión 🙂

Empezaremos viendo lo que son las igualdades, las identidades y las ecuaciones y las diferencias que hay entre ellas.

Luego veremos lo que son las soluciones, los grados y los términos de una ecuación. A continuación, veremos lo que son las ecuaciones equivalentes, que es en lo que se sustenta toda su resolución.

Luego ya pasaremos a ver los tipos de ecuaciones: de primer grado, de segundo grado, bicuadradas y de tercer grado, y por supuesto la resolución de todos estos estos tipos. 

IGUALDAD

En todas estas expresiones aparece el signo = y se llaman igualdades.

IGUALDAD NUMERICA E IGUALDAD LITERAL 

La igualdad 2 · 5 = 10 es una igualdad numérica porque sólo aparecen números (no letras)

Las igualdades:

x + 2x = 3x

x – 6 = 4

son igualdades literales porque contienen expresiones algebraicas (números mezclados con letras)

MIEMBROS DE UNA IGUALDAD 

En todas las igualdades hay dos miembros:

El primer miembro: es la expresión que hay antes del signo =

El segundo miembro: es la expresión que hay después del signo =

Para reforzar mira el siguiente VIDEO

Experimenta en PHET 

Desarrolla la siguiente actividad en LIVEWORKSHEETS